In an earlier section, the idea of the hazard rate (or hazard function) was introduced as the frequency at which the event of interest occurs per unit of time. If we want to put this into strict mathematical terms, we can:

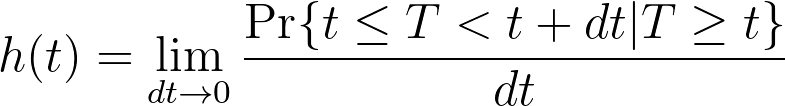
In words, this suggests that the hazard rate (h(t)) is equal to the probability that the event of interest occurs in some small window of time between [t, t + dt), given that the event of interest didn’t occur prior to time t. This is considered an instantaneous hazard rate since the window of time defined by dt is considered to be extremely small (infinitesimally small, approaching zero).

Using Bayes theorem and simplifying this expression (not shown here), the hazard function can also be defined using the previously defined pdf and survival function:

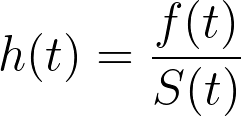
In this form, the hazard function can be interpreted as the density of events at time t divided by the probability that the event of interest has not occurred by time t.

Note again that - if we knew the functional form of the pdf f(t), we would be able to directly calculate the form of the hazard function. However, Cox proportional hazards regression makes no assumption about this pdf, and is as a result a semiparametric analysis.