In a previous section, we provided the definition for the survival function:
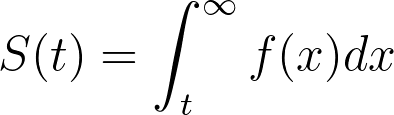
Or, equivalently:
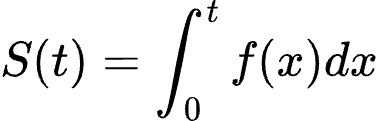
Taking the derivative of both sides, we see that:
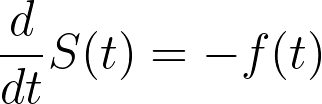
This is useful because the derivative of a logarithm of a function can be defined as:
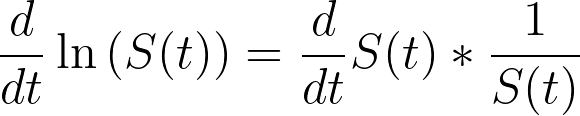
If we start replacing terms in the equation above, we can simplify this expression:
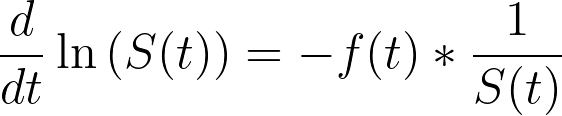
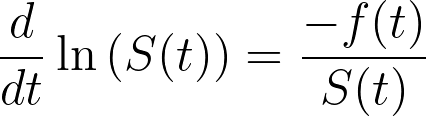
Which is the negative of the formula that we provided for the hazard function in the previous section:
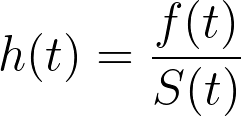
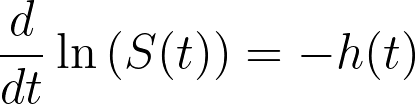
If we integrate and exponentiate the left side of the equation, we arrive at a definition of the survival function in terms of the hazard rate:
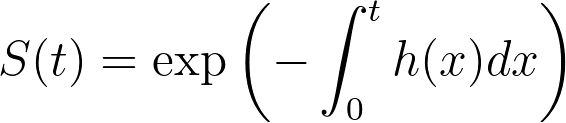
Let’s now define the integral in the equation above as a new concept known as the cumulative hazard function, or the cumulative hazard rate, denoted by H(t) (note the use of the capital H for the cumulative hazard rate compared to the lower-case h for the instantaneous hazard rate):
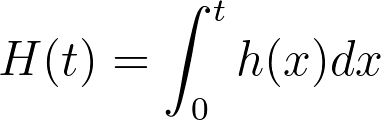
This cumulative hazard function can be thought of as providing the total accumulated risk of experiencing the event of interest that has been gained by progressing to time t. While the instantaneous hazard rate (h(t)) can increase or decrease with time, the cumulative hazard rate can only increase or remain the same. Mathematically, this is because the instantaneous hazard rate must be greater than or equal to zero. But conceptually, this makes sense as the “total accumulated” risk of experiencing the event of interest should only ever increase (or stay the same) over time.
Putting it all together, we arrive at a definition of the survival function that uses the cumulative hazard function:
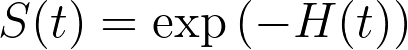
Or, equivalently:

These two equations let us quickly convert between the survival function (the probability that the event of interest has not occurred by time t) and the cumulative hazard function (the total accumulated risk of experiencing the event of interest by time t), and it should make sense that these two concepts are closely related.