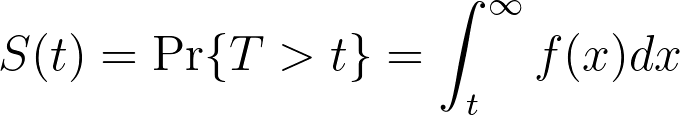When performing survival analysis, the response variable is the elapsed amount of time that passes until the event of interest occurs. This variable is continuous (meaning it can take on any number of different values), and its values cannot be negative. We will call this variable T (capital T to indicate that it is the random variable for elapsed time whose value is unknown. In comparison, specific time points will be denoted with a lowercase t). Although the values of T are unknown, this variable can be defined using a probability density function (pdf) called f(t), and a cumulative distribution function (cdf) called F(t).

Direct interpretation of a pdf can be a little confusing at first, and is beyond the scope of what we’re going to cover in this guide. However, there are a few important facts to note about pdf’s before we move on:

1.The value of f(t) is positive (greater than or equal to zero) for all values of t

2.The area under the curve of f(t) covering all possible values of T is equal to one

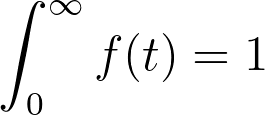
3.The relationship between the pdf and the cdf is given by

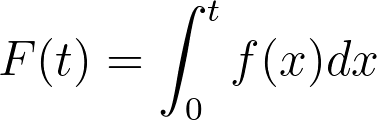
Using these facts about the pdf and cdf, we can provide a relatively easy-to-understand interpretation of F(t): it is the probability that the event of interest has occurred by (and including) time t. Mathematically:

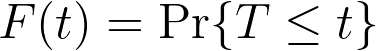
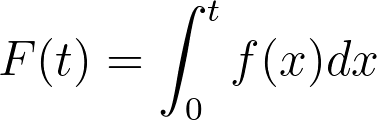
In other words, F(t) gives the probability that the observed elapsed time T is less than the specific time t being evaluated in the expression. However in survival analysis, we’re generally not interested in the probability that the event has occurred by a specific time. Rather, we would like to know the probability that the event has not occurred by a specific time. We can use a few of the facts presented earlier about the pdf and the cdf to give this mathematical form.

We know that the area under the curve of the pdf over all values of t is equal to one:

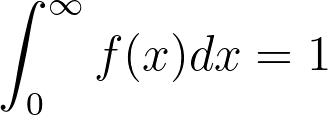
If we know that the cdf is the probability that the event has occurred by time t, then the complement of the cdf must be the probability that the event has not occurred by time t, and we can build the following relationship:

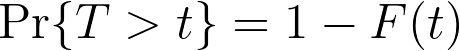
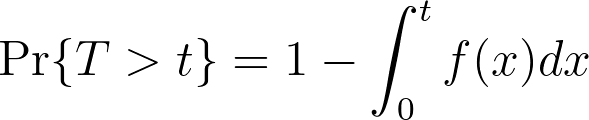
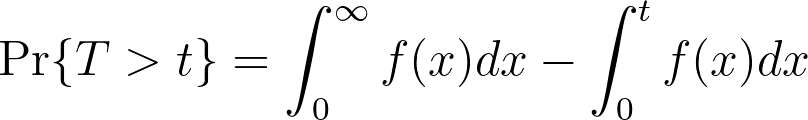
This is known as the survival function, or S(t), and gives the probability that the event of interest has not occurred by elapsed time t.