While the theoretical basis of Akaike's method is difficult to follow, it is easy to do the computations and make sense of the results.
The fit of any model to a data set can be summarized by an information criterion developed by Akaike, called the AIC. If you accept the usual assumptions of nonlinear regression (that the scatter of points around the curve follows a Gaussian distribution), the AIC is defined by a simple equation from the sum-of-squares and number of degrees of freedom of the two models. It is not possible to make sense of this AIC value itself, because its units depend on which units you use for your data.
To compare models, it is only the difference between the two AIC values that matter. When you take the difference, the units cancel out and the result is unitless.

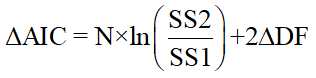
The equation now makes intuitive sense. Like the F test, it balances the change in goodness-of-fit as assessed by sum-of-squares with the change in the number of degrees of freedom (due to differences in the number of parameters to be fit). Since model 1 is the simpler model, it will almost always fit worse, so SS1 will be greater than SS2. Since the logarithm of a fraction is always negative, the first term will be negative. Model 1 has fewer parameters and so has more degrees of freedom, making the last term positive. If the net result is negative, that means that the difference in sum-of-squares is more than expected based on the difference in number of parameters, so you conclude that the more complicated model is more likely.
Prism reports the difference between the two AICc values as the AICc of the simpler model minus the AICc of the more complicated model. When the more complicated (more parameters) model has the lower AICc and so is preferred, Prism reports the difference of AICc as a positive number. When the simpler model has the lower AICc and so is preferred, Prism reports the difference of AICc as a negative number.
The equation above helps you get a sense of how AIC works – balancing change in goodness-of-fit vs. the difference in number of parameters. But you don’t have to use that equation. Just look at the individual AIC values, and choose the model with the smallest AIC value. That model is most likely to be correct.
Prism actually doesn't report the AIC, but rather the AICc. That value includes a correction for low sample size. The equation is a bit more complicated, and is more accurate with small sample size. With larger sample sizes, the AIC and AICc are almost the same.
Note that these calculations are based on information theory, and do not use the traditional “hypothesis testing” statistical paradigm. Therefore there is no P value, no conclusion about “statistical significance”, and no “rejection” of a model.
From the difference in AICc values, Prism calculates and reports the probability that each model is correct, with the probabilities summing to 100%. If one model is much more likely to be correct than the other (say, 1% vs. 99%), you will want to choose it. If the difference in likelihood is not very big (say, 40% vs. 60%), you will know that either model might be correct, so will want to collect more data. These probabilities are computed with this equation, where Δ is the difference between the AICc values.

Note that this method simply compares the fits of the two models you chose. It is possible that a third model, one you didn't choose, fits far better than either model you chose.