What does "ambiguous" mean?

"Ambiguous" is a term coined by GraphPad to describe a fit that doesn't really nail down the values of all the parameters.

Changing the value of any parameter will always move the curve further from the data and increase the sum-of-squares. But when the fit is 'ambiguous', changing other parameters can move the curve so it is near the data again. In other words, many combinations of parameter values lead to curves that fit equally well.

Prism puts the word 'ambiguous' in the top row of results. For the parameters that are 'ambiguous' (there may be one or several), Prism puts '~' before the best fit values and standard errors, and reports "very wide" for the corresponding confidence intervals.

If you check the option in the diagnostics tab to report dependency, the value will be >0.9999 for all the 'ambiguous' parameters (that is how we define 'ambiguous'; the threshold value is arbitrary).

If the fit is 'ambiguous' you really can't interpret the best-fit values of some parameters.

Does it matter?

If your goal is to interpolate unknowns from a standard curve, you won't care that the parameter values are 'ambiguous'. So long as the curve goes through the points, and doesn't wiggle too much, the interpolations will be useful.

If your goal is to learn about your data by inspecting the values of the parameters, then you've got a real problem. At least one of the parameters has a best-fit value that you should not rely upon.

But the R2 is really high...

In many cases, the R2 will be really high, maybe 0.99. That just means that the curve comes close to the data points. It doesn't mean the data define all the parameters. If the fit is 'ambiguous', you can get an equally well-fitting curve with a different set of values of the parameters.

Reasons for ambiguous fits

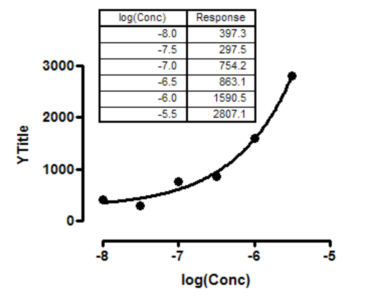
Data not collected over a wide enough range of X values

The data above show a fit of a dose-response curve to a set of data that don't define a top plateau. Since the top plateau was not constrained to a constant value, Prism reports the fit to be ambiguous.

Model too complicated for the data

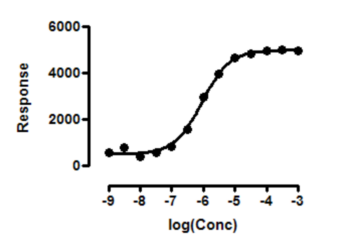
The data above fit fine to a standard dose-response curve. But if you try to fit it to a biphasic dose-response curve, Prism reports that the results are ambiguous. The data follow a standard dose-response model just fine, with no evidence of a second component. So fitting to a biphasic model -- with two EC50 values -- is ambiguous.

Model has redundant parameters

The simplest example would be fitting this model: Y= A + B + C*X. This model describes a straight line with a slope equal to C and a Y intercept equal to the sum of A and B. But there is nothing in the data to fit A and B individually. There are an infinite number of pairs of values of A and B that lead to the same sum, so the same Y intercept. If Prism attempts to fit this model, it will conclude that the fit is ambiguous.

Prism cannot tell the difference between this case and the previous one. But the two cases are distinct. The model in this example has redundant parameters. It doesn't matter what the data look like, or how many data points you collect, fitting this model will always result in 'ambiguous' results, because two of the parameters are intertwined. In the previous example, the fit was ambiguous with the example data set, but would not have been ambiguous with other data sets.

Checklist

Can you constrain any parameters to a constant value?

Can you share one or more parameters among datasets?

Can you collect more data points, perhaps over a wider range of X values?

If your model has two phases or components, consider switching to a one phase or component model.