Median survival time

The median survival time is the time point at which the probability of survival equals 50%. Some things to keep in mind:

•If the probability of survival exceeds 50% at the longest time point, then the median survival time cannot be computed. Prism reports that the median survival is “undefined”. The logrank comparison of curves compares entire curves, and does not compare median survival times. So the P value computed by the logrank test is still valid even if one or both median survival times are undefined

•If the survival curve is horizontal at 50% survival, then the median survival time is not clearly defined. In the survival curve below, the curve is horizontal at Y=50% between 9 and 17 months. Prism follows the suggestion of Machin and reports that the median survival is the average of those two values, or 13 months in this case.

The 95% confidence interval of median survival

When calculating the median survival, Prism will also report the 95% confidence interval for this estimate (requires Prism 10.5 or newer and a subscription with a named-user license). The method that Prism uses to calculate the 95% confidence interval for median survival is described by Brookmeyer and Crowley (1982). The mathematical details are sufficiently advanced as to be omitted in this text. The general idea is that Prism identifies values for which the following inequality holds true:

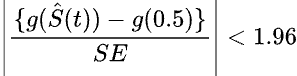
Where S(t) is the Kaplan-Meier survival estimate at time t, g() is a transformation function, and SE is the standard error of the transformed survival function. Specifically in Prism, the complementary log-log transformation is used for g, resulting in this inequality taking the following form:

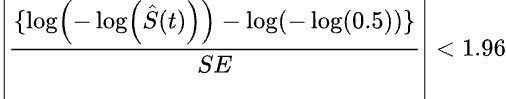
The general idea here is that the times for which this inequality holds true are plausible values of the true median, while the boundaries represent upper and lower times for the 95% confidence interval of the median. Note that the lower boundary may be equal to zero, while the upper boundary may not be defined (reported as "+infinity" in Prism).

To read more (including information about different choices for the transformation method and calculation of the standard error):

•Talsma, P. A. (2023). Estimation of median survival time and its 95% confidence interval using SAS PROC LIFETEST. Journal of Biopharmaceutical Statistics, 34(3), 366–378.

•Brookmeer and Crowley, A confidence interval for the median survival time. Biometrics (1982) vol. 38 (1) pp. 29-41.

•Barker reviews several methods and points out how different their results can be. The Mean, Median, and Confidence Intervals of the Kaplan-Meier Survival Estimate—Computations and Applications. The American Statistician (2009) vol. 63 (1) pp. 78-80

Calculation of median survival time assumes "stairstep"

Prism - like most programs - defines median survival as the time at which the staircase survival curve crosses 50% survival. This is an accurate statement of median survival in the subjects or animals actually included in the data set. The graph on the left below shows how Prism computes median survival (211 days for this example). If you connected the survival times with point-to-point lines rather than a staircase, you’d find that the line may intersect Y=50% at an earlier time, and thus you’d come up with a different value for median survival (193 days in the example on the right below). This would make sense if you were trying to predict median survival for future patients. Prism does not do this, as it is not standard