Introduction

You can determine the equilibrium dissociation constant of an unlabelled ligand by measuring its competition for radioligand binding.

Step by step

Create an XY data table. Enter the logarithm of the concentration of the unlabeled compound into X, and binding into Y. If you have several experimental conditions, place the first into column A, the second into column B, etc. Use subcolumns to enter replicates.

From the data table, click Analyze, choose nonlinear regression, choose the panel of Competition Binding equations, and choose One site - Fit Ki.

You must constrain two parameters to constant values based on your experimental design:

•RadioligandNM is the concentration of labeled ligand in nM. A single concentration of radioligand is used for the entire experiment.

•HotKdNM is the equilibrium dissociation constant of the labeled ligand in nM.

Model

logEC50=log(10^logKi*(1+RadioligandNM/HotKdNM))

Y=Bottom + (Top-Bottom)/(1+10^(X-LogEC50))

 

 

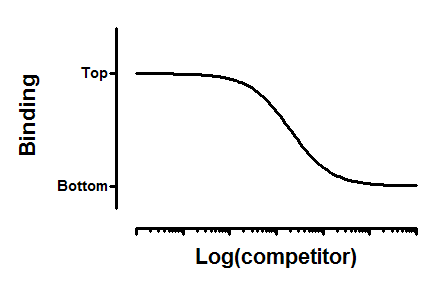
Interpret the parameters

Top and Bottom are plateaus in the units of Y axis.

logKI is the log of the molar equilibrium dissociation constant of unlabeled ligand.

Ki is the equilibrium dissociation constant in Molar.

Notes

This model fits the Ki of the unlabelled ligand directly. It does not report the EC50, so you do not need to apply the Cheng and Prusoff correction(1). Instead you enter the concentration of radioligand and its Kd as constants, and Prism directly fits the Ki of your cold compound. If you want to know the IC50, fit a log(dose)-response curve.

If you want to know the IC50 (which is not very informative in this situation) fit the data using an alternative equation.

The analysis assumes that you have one site, and that the binding is reversible and at equilibrium.

 

1. Cheng, Y. and Prusoff, W. H. Relationship between the inhibition constant (K1) and the concentration of inhibitor which causes 50 per cent inhibition (I50) of an enzymatic reaction. Biochem Pharmacol, 22: 3099-3108, 1973.