Approach to comparing models
Which model is 'best'? At first, the answer seems simple. The goal of nonlinear regression is to minimize the sum-of-squares, so the model with the smaller sum-of-squares clearly fits best. But that is too simple.
The model with fewer parameters almost always fits the data worse. When you compare two models, the simpler model (with fewer parameters) will have a higher sum-of-squares. When you compare datasets, the global fit will have a higher sum-of-squares than the sum of the individual fits. And when you compare fits with and without a parameter constrained to a particular value, will have a higher sum-of-squares than a model where you don't constrain the parameter.
Both the F test and the AIC method take into account both the difference in goodness-of-fit but also the number of parameters. The question is whether the decrease in sum of squares (moving from simpler to more complicated model) is worth the 'cost' of having more parameters to fit. The F test and AICc methods approach this question differently.
How Prism reports model comparison
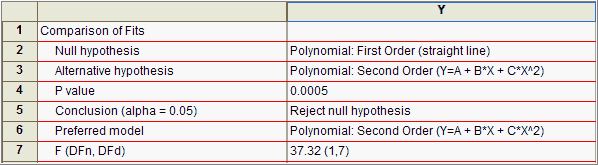
Prism reports the results for the comparison at the top of the nonlinear regression table of results. It clearly states the null and alternative hypotheses. If you chose the F test, it reports the F ratio and P value. If you chose Akaike's method, it reports the difference in AICc and the probability that each model is correct.
Finally, Prism reports the 'preferred' model. You should understand how Prism decides which model is 'preferred' as you may 'prefer' the other model.
If you chose the extra sum-of-squares F test, then Prism computes a P value that answers this question:
If the null hypothesis is really correct, in what fraction of experiments (the size of yours) will the difference in sum-of-squares be as large as you observed or larger?
In the Compare tab, you also tell Prism which P value to use as the cut off (the default is 0.05). If the P value is lower than that value, Prism chooses the more complicated model. Otherwise it chooses the simpler model.
If you chose Akaike's method, Prism chooses the model that is more likely to be correct. But you should look at the two probabilities. If they are similar in value, then the evidence is not persuasive and both models fit pretty well.
Analysis checklist for comparing models
Was it possible to fit both models?
Before running the extra sum-of-squares F test or computing AICc values, Prism first does some common sense comparisons. If Prism is unable to fit either model, or if either fit is ambiguous or perfect, then Prism does not compare models.
Are both fits sensible?
Apply a reality check before accepting Prism's results. If one of the fits has results that are scientifically invalid, then accept the other model regardless of the results of the F test or AIC comparison.
For example, you would not want to accept a two-phase exponential model if the magnitude of one of the phases is only a tiny fraction of the total response (especially if you don't have many data points). And you wouldn't want to accept a model if the half-life of one of the phases has a value much less than your first time point or far beyond your last time point.
Analysis checklist for the preferred model
Before accepting the 'preferred' model, you should think about the same set of questions as you would when only fitting one model. You can consult the detailed checklist or the abbreviated version below.
How precise are the best-fit parameter values?
Are the confidence bands 'too wide'?
Does the residual plot look good?
Does the scatter of points around the best-fit curve follow a Gaussian distribution?
